Risikodiversifizierung
Risikodiversifizierung (auch Risikodiversifikation) ist eine Strategie, mit der ein Kapitalmarktteilnehmer das Risiko einer Teilnahme auf dem Kapitalmarkt durch die Aufteilung seines Vermögens auf verschiedene Vermögenswerte (sog. Assets) reduzieren kann.
Die Strategie der Diversifikation kommt in vielen Wirtschaftsbereichen zum Einsatz, zum Beispiel im Absatz- und Beschaffungsbereich. Ein anderes Beispiel ist das diversifizierte Humankapital: Anstatt ein Einzelunternehmen zu gründen, kann ein Unternehmen auch aus mehreren Mitgliedern bestehen, sodass Fehlentscheidungen vorgebeugt werden kann. Allen Anwendungsgebieten liegt jedoch ein Gedanke zu Grunde: Durch Diversifikation soll das Risiko reduziert werden.[1]
Inhaltsverzeichnis
Entwicklung von der Grundidee zur Portfoliozusammenstellung
Naive Diversifikation
Das angelsächsische Sprichwort „Don´t put all your eggs in one basket.“, das deutsche Sprichwort „Man soll nicht alles auf eine Karte setzen.“ und Erasmus´ Warnung im 14. Jahrhundert „Vertraue nicht all deine Waren einem einzigen Schiff an.“ sind Hinweise auf ein lange tradiertes Wissen über die Möglichkeit der Risikominderung durch Diversifikation.[2] [3]
Talmudische ⅓-Regel
Der babylonische Talmud enthält eine frühe Handlungsanweisung zur Aufteilung eines Vermögens in Anlagenformen mit unterschiedlicher Liquidität und unterschiedlichem Risiko. In der deutschsprachigen Fassung von Lazarus Goldschmidt heißt es:
Ferner sagte R. Jiçhaq: "Stets teile ein Mensch sein Geld in drei Teile: ein Drittel in Grundbesitz, ein Drittel in Waren und ein Drittel in seiner Hand."
[4]
Diese, auch als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \textstyle\frac{1}{3}}
- Regel bekannte, etwa anderthalb bis zwei Jahrtausende alte Anweisung geht auf die im Hintergrund liegenden Überlegungen nicht weiter ein. Sie wird gelegentlich auf die heutige Situation übertragen als ein Rat, ein Drittel in Immobilien anzulegen, ein weiteres Drittel in Aktien zu investieren und ein Drittel liquide, oder in Form von Staatsanleihen zu halten. Eine weitere Übertragung ist die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \textstyle\frac{1}{N}}
- Regel, die Investition ohne Rückgriff auf die Eigenschaften der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle N}
modellhaft gleichmäßig verteilten, verfügbaren Assets.Referenzfehler: Für ein <ref>-Tag fehlt ein schließendes </ref>-Tag.
Experimentell fanden Benartzi und Thaler, dass ein substantieller Anteil von Personen, die in Defined Contribution Saving Plans investierten, implizit nach einer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \textstyle\frac{1}{N}}
-Regel entschied.[5]
Portfolio-Selection Modell von Markowitz
Ausgangspunkt ist, dass ein Investor sein Kapital auf unterschiedliche, risikobehaftete Anlagen aufteilen kann und dabei stets im Zielkonflikt zwischen Risiko und Rendite steht. Die naive Diversifikation lässt den erwarteten Ertrag und das Risiko, insbesondere die Korrelation der Risiken, unberücksichtigt. In den Jahren 1950 - 1970 untersuchte die angelsächsische Forschung das Problem der optimalen Diversifikation, woraus sich die klassische Portfoliotheorie entwickelte. Die ersten Ideen zu diesem Thema publizierte Markowitz 1952 im Journal of Finance. 1959 stellte er in seinem Buch Portfolio Selection: Efficient Diversification of Investments das sogenannte Portfolio-Selection-Modell vor, mit dem sich effiziente Portfolios herleiten lassen. Unter anderem Roy, Sharpe und Tobin entwickelten anschließend daraus die klassische Portfoliotheorie, welche das Problem korrelierter Risiken unter einigen Annahmen zunächst einmal löste.
Im Gegensatz zur naiven Diversifikation ist die klassische Portfoliotheorie durch ein bedeutendes Element gekennzeichnet: Die Diversifikation wird mit Hilfe der Wahrscheinlichkeitsrechnung und der Statistik untersucht. Das Portfolio-Selection Modell von Markowitz ist ein stochastisches Ein-Perioden-Modell. Die Erträge der einzelnen Assets im Portfolio sind korrelierte Zufallsvariablen und der risikoscheue Investor orientiert sich im Zielkonflikt zwischen erwarteter Rendite und Risiko bei seiner Entscheidung über ein Portfolio ausschließlich am Erwartungswert und an der Standardabweichung (auch Volatilität) der Portfolio-Rendite. Im Kern geht es somit um die Abweichung der Zufallsvariable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle X}
von ihrem Erwartungswert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \operatorname {E}(X)}
. Wie bereits erwähnt, ist die Zufallsvariable in diesem Fall die Rendite. Diese berechnet sich aus der Relation zwischen der Summe aus der Kursentwicklung und der Dividende und dem eingesetzten Kapital. Die Rendite bezieht sich stets auf die Zukunft. Da die Zukunft ungewiss ist, wird die durchschnittliche Rendite aus der Vergangenheit mit dem Erwartungswert der zukünftigen Rendite gleichgesetzt. Analog entspricht die zukünftige Standardabweichung der vergangenen Abweichung. Je höher die Standardabweichung ist, desto größer ist die Wahrscheinlichkeit, dass der Erwartungswert nicht eintritt bzw. ein höherer Verlust entsteht.[3] [6]
Die Erwartungsbildung eines Investors kann jedoch auch auf Informationen beruhen, die aus einem Research oder einer Finanzanalyse resultieren.[2]
Markowitz zeigte in seinem Modell, dass es in Abhängigkeit von der Risikobereitschaft des Investors vorteilhafter sein kann, in mehrere verschiedene Anlagen zu investieren, anstatt eine Investition in nur eine Anlage mit der höchsten erwarteten Rendite zu tätigen. [2]
Das Modell geht von einem vollkommenen Kapitalmarkt aus. Weitere Prämissen des Modells lauten:[7]
- Der Markt ist informationseffizient. Das bedeutet, dass die Marktteilnehmer die gleichen Informationen besitzen und sie gleich verarbeiten.
- Der Investor handelt rational und nutzenmaximierend.
- Alle Marktteilnehmer haben einen Marktzugang.
- Es existieren weder Steuern noch Transaktionskosten.
- Alle Wertpapiere sind beliebig teilbar. Demnach existieren auch halbe Aktien.
Das wichtigste Ergebnis von Markowitz lautet, dass das Portfoliorisiko nicht dem durchschnittlichen Risiko seiner Bestandteile entspricht, sondern durch die Korrelationskoeffizienten dieser Bestandteile bestimmt wird. [2]
Zusammenfassend bedeutet es, dass der im Folgenden dargestellte Diversifikationseffekt durch drei Parameter gekennzeichnet wird: durch die erwartete Rendite, die Streuung und durch den Korrelationskoeffizienten.[2]
Die Anfänge der klassischen Portfoliotheorie stellten einen Meilenstein in der Finanzierungstheorie dar, da durch die Kalkulation von Risiken und Renditen Empfehlungen zu Finanzanlagen gegeben werden konnten. Deshalb wird die Portfolio-Theorie auch als normative Theorie bezeichnet. Sie bildet aber auch die Grundlage für die neoklassische Finanzierungstheorie. Aus dem Fondsmanagement und dem Versicherungswesen ist die Portfoliotheorie außerdem nicht mehr wegzudenken. [2] [8]
Diversifikationseffekt
Entgegen der weit verbreiteten Auffassung, Diversifikation ziehe einen Chancenverzicht nach sich, illustriert die Portfoliotheorie, dass eine kostenlose Diversifikation möglich ist. "Kostenlos" bedeutet in diesem Zusammenhang, dass die Diversifikation keine negativen Auswirkungen auf den Ertrag hat. Voraussetzung ist, dass richtig diversifiziert wird.[1] Übernimmt dagegen ein Anleger Risiken, die er durch Diversifikation ausschalten könnte, entsteht ihm ein Nachteil, der mit einem unnötigen Nutzenentgang verbunden ist. [2]
Im Folgenden werden die theoretischen Hintergründe der richtigen Diversifizierung dargestellt und mit Hilfe eines Beispiels veranschaulicht. Dabei geht es im Kern um die Untersuchung des Portfoliorisikos bei einer Investition in zwei unterschiedliche, risikobehaftete Wertpapiere.[1]
- Beispiel: Für die Aktien der Dresdner Bank und Volkswagen wurden jeweils der Erwartungswert der Rendite und die Standardabweichung geschätzt. Die Schätzung beruht auf einer Stichprobe von April 1978 bis März 1998. Die Renditen seien normalverteilt. [1]
| statistische Maßgröße | Dresdner Bank | Volkswagen |
|---|---|---|
| Erwartungswert der Rendite (in %) | 0,81 | 1,19 |
| Standardabweichung (in %-Punkten) | 7,10 | 8,41 |
- Müsste sich ein risikofreudiger Anleger zwischen den beiden Anlagen entscheiden, würde er sich für die VW-Aktie entscheiden. Ein risikoscheuer Investor würde dagegen die Aktie der Dresdner Bank wählen.
- Es stellt sich jedoch die Frage, wie sich ein Investor entscheiden würde, wenn er beide Aktienwerte halten sollte.[1] Dies ist die zentrale Frage, der im Folgenden nachgegangen werden soll.
- Bei einem naiv diversifizierten Portfolio würde der Investor sein Kapital gleichmäßig auf die beiden Aktienwerte aufteilen. Er würde folglich 50% seines Vermögens in die VW-Aktie und 50% in die Dresdner Bank-Aktie investieren.[1]
Die Portfoliorendite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mu_p}
lässt sich mit Hilfe der folgenden Formel berechnen:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mu_p =\sum_{i=1}^m x_i \mu_i }
mit
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle m\,} : Wertpapieranzahl im Portfolio
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_i\,} : Anteil des Wertpapiers i am Portfolio
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mu_i\,} : erwartete Rendite des Wertpapiers i.
Der Erwartungswert der Portfoliorendite errechnet sich somit aus der Addition der gewichteten Erwartungswerte der Einzelinvestitionen.[7]
Für einen 2-Anlagen-Fall gilt dementsprechend:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mu_p\,= x_1 \mu_1 + x_2 \mu_2} .
Die relativen Portfolio-Anteile müssen definitionsmäßig zusammen 1 ergeben. Es muss somit stets die folgende Bedingung gelten:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sum_{i=1}^m x_i = 1\,} .
Das Portfoliorisiko berechnet sich aus der Summe der gewichteten Einzelrisiken. Zusätzlich muss der stochastische Zusammenhang zwischen den Renditen, der Korrelationskoeffizient, berücksichtigt werden. Dies war, wie oben erwähnt, eine zentrale Erkenntnis der Portfoliotheorie.
Für den 2-Anlagen-Fall lässt sich das Portfoliorisiko Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sigma_p\,}
mit dieser Formel berechnen: [7]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sigma_p = \sqrt{{x_1}^2 {\sigma_1}^2 + {x_2}^2 {\sigma_2}^2 + 2 x_1 x_2 \sigma_1\sigma_2 \rho_{{1}{2}} }}
mit
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_1\,} : Anteil des Wertpapiers 1 am Portfolio
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_2\,} : Anteil des Wertpapiers 2 am Portfolio
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sigma_1\,} : Standardabweichung des Wertpapiers 1
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sigma_2\,} : Standardabweichung des Wertpapiers 2
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \rho_{{1}{2}}\,} : Korrelationskoeffizient der Wertpapiere 1 und 2.
Die gegenseitige Abhängigkeit der Renditen wird mit dem Korrelationskoeffizienten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \rho} gemessen.Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \rho} liegt in dem Intervall von -1 bis +1. Der Wert +1 bedeutet, dass sich die Renditen gleichgerichtet verhalten. Zwischen ihnen besteht folglich ein sehr ausgeprägter, positiver Zusammenhang. Entwickeln sich die Renditen dagegen perfekt entgegengesetzt, beträgt der Korrelationskoeffizient -1. Der Korrelationskoeffizient kann auch den Wert 0 annehmen. In diesem Fall sind die Renditen unkorreliert, sodass zwischen ihnen kein systematischer Zusammenhang existiert.[1] Wenn der Korrelationskoeffizient einen Wert annimmt, der kleiner als +1 ist, dann sinkt die Volatilität des Portfolios unter das arithmetische Mittel der Risiken der Portfoliobestandteile. Die Senkung der Volatilität und somit die Risikominimierung wird als Diversifikationseffekt bezeichnet. Dieser ist in Abhängigkeit des Korrelationskoeffizienten unterschiedlich stark ausgeprägt. Wird eine Diversifikation planvoll und gezielt vorgenommen (sog. Asset Allocation), d.h. nicht naiv, kann durch die richtige Wahl des Mischungsverhältnisses das Risiko nahezu komplett ausgeschaltet werden. Dies wird dann der Fall sein, wenn sich die Renditen perfekt gegenläufig entwickeln.[1] [7]
Portfolio-Möglichkeitenkurven
Der Diversifikationseffekt lässt sich mit sogenannten Portfolio-Möglichkeitenkurven veranschaulichen. Dazu werden im Ertrags-Risiko-Diagramm zunächst Portfolios eingetragen, die zu 100 % aus einem Aktienwert bestehen. Auf der Abszissenachse im Ertrags-Risiko-Diagramm wird das Portfoliorisiko und auf der Ordinatenachse die erwartete Portfoliorendite abgetragen. Der Punkt A in der Grafik " Wirkung des Korrelationskoeffizienten: Portfolio-Möglichkeitenkurven " stellt dabei den Ertragswert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mu_A\,}
und das Risiko Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sigma_A\,}
eines Portfolios dar, die sich ergeben, wenn der Kapitalmarktteilnehmer sein zur Verfügung stehendes Anlagevermögen in nur ein Wertpapier investiert. Entsprechendes gilt für den Punkt B. Im nächsten Schritt werden die Portfoliorendite und das Portfoliorisiko für unterschiedliche Mischungsverhältnisse berechnet und in das Ertrags-Risiko-Diagramm übertragen. In Abhängigkeit davon, welchen Wert der Korrelationskoeffizient Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \rho_{AB}\,}
annimmt, entsteht eine unterschiedlich stark ausgeprägte Portfolio-Möglichkeitenkurve. Diese wird in der Literatur auch als Opportunitätslinie oder Portefeuillelinie bezeichnet.[1] [7]
Bei Anlagen, deren Renditen einen Korrelationskoeffizienten von -1 aufweisen, ist das Portfolio risikolos, da die negativen Erträge der einen Anlage durch die positiven Erträgen der anderen Anlage vollständig kompensiert werden. Die Rendite kann somit als sicher betrachtet werden. Die Portfolio-Möglichkeitenkurve ist in diesem Fall spitz zulaufend. Punkt C in der Grafik veranschaulicht den entstehenden maximalen Diversifikationseffekt.[1] [7]
Sind die Renditen der Wertpapiere perfekt positiv korreliert (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \rho_{AB}\,}
= +1), d.h. dass bei beiden Anlagen gleichzeitig positive bzw. negative Renditen auftreten, tritt kein Diversifikationseffekt ein, da alle möglichen Ertrags-Risiko-Kombinationen des Portfolios auf der Verbindungsgeraden zwischen den Punkten A und B liegen: Erwartet der Investor eine höhere Rendite, steigt das Risiko zwangsweise an. Das Portfoliorisiko entspricht in diesem Fall dem durchschnittlichen Risiko der Anlagen.[7]
Die vorgestellten Portfolio-Möglichkeitenkurven stellen theoretische Sonderfälle dar. Häufig verläuft die Portfolio-Möglichkeitenkurve jedoch hyperbelförmig. Dies ist dann der Fall, wenn der Korrelationskoeffizient der Renditen von zwei Wertpapieren in dem Intervall von -1 und +1 liegt.[1]
- Für das Portfolio, das aus VW- und Dresdner Bank-Aktien besteht, ergibt sich ein Korrelationskoeffizient von 0,4974. Mithilfe des Korrelationskoeffizienten lassen sich durch die Variation des Mischungsverhältnisses verschiedene Positionen im Ertrags-Risiko-Diagramm berechnen. Die folgende Tabelle gibt die Ergebnisse der Berechnung für einige Mischungsverhältnisse beispielhaft wieder.[1]
| Portfolio-Anteil Dresdner Bank | Rendite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mu\,} | Risiko Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sigma\,} |
|---|---|---|
| 0% | 1,19 | 8,41 |
| 10% | 1,15 | 7,94 |
| 25% | 1,10 | 7,35 |
| 50% | 1,00 | 6,72 |
| 65% | 0,95 | 6,59 |
| 75% | 0,91 | 6,63 |
| 90% | 0,85 | 6,85 |
| 100% | 0,81 | 7,10 |
- Überträgt man diese Werte in ein Ertrags-Risiko-Diagramm, ergibt sich eine hyperbelförmige, nach rechts geöffnete Kurve, die alle Wertpapierkombinationen und die dazugehörigen Portfoliorisiken und die erwarteten Portfoliorenditen enthält.[1]
Der hyperbelförmige Verlauf der Portfolio-Möglichkeitenkurve ist der Regelfall. Somit entwickeln sich die Renditen grundsätzlich gleichgerichtet. [1] Dies liegt daran, dass es Faktoren gibt, die sich auf alle Wertpapiere auswirken. Lediglich die Intensität der Beeinflussung ist unterschiedlich. Zu diesen Faktoren zählen beispielsweise die Inflation und eine schwere Rezession, die zu einem Nachfrageeinbruch bei den meisten Unternehmen führt. Das bedeutet, dass auch bei einem diversifizierten Portfolio immer ein gewisses Restrisiko verbleibt. [9]
Jede hyperbelförmige Portfolio-Möglichkeitenkurve weist einen charakteristischen Punkt auf, den Scheitelpunkt. In der Grafik " Wirkung des Korrelationskoeffizienten: Portfolio-Möglichkeitenkurven. " ist das der rot markierte Punkt M.
- Im Beipielportfolio stellt dieser Punkt ein Portfolio dar, das zu 65 % aus Dresdner Bank-Aktien und zu 35 % aus VW-Aktien besteht.
Bei diesem Mischungsverhältnis ist das Risiko des Portfolios bzw. die Volatilität, am geringsten. Man spricht vom globalen Minimum-Varianz-Portfolio, oder auch vom Safety-First-Portfolio.
Je stärker sich der Korrelationskoeffizient der -1 nähert, desto stärker ist die Krümmung der Portfolio-Möglichkeitenkurve und desto stärker ist die Ausprägung des Diversifikationseffektes. Je gegenläufiger sich die Renditen somit zueinander verhalten, desto mehr Risiko kann bei der Mischung der Anlagen eliminiert werden. In der Grafik wird ersichtlich, dass bei bestimmten Mischungsverhältnissen das Portfoliorisiko sogar unter das niedrigste Risiko der beiden Wertpapiere fällt, in diesem Fall unter das Risiko von Wertpapier A. [1] [7]
Die dargestellten Gesetzmäßigkeiten gelten bei allen volatilen Anlageformen und somit nicht nur bei Aktien oder Anleihen, sondern beispielsweise auch bei Immobilien.[3]
Bisher wurde der Diversifikationseffekt für die Mischung von zwei Anlagen dargestellt. Wählt ein Investor mehr als zwei Anlagen, dann lässt sich arithmetisch zeigen, dass sich eine vollständige Diversifikation erzielen lässt. Es verbleibt jedoch immer ein gewisses Risiko, das nicht eliminiert werden kann. Dieses Risiko wird als systematisches Risiko bezeichnet. Das Risiko, das durch die Diversifikation eliminiert wird, ist das unsystematische Risiko. In der Praxis wird es bei einer Wertpapieranzahl von circa 15 eliminiert.[1]
Effiziente Portfolios
Die Portfolio-Möglichkeitenkurve für die VW- und Dresdner Bank-Aktien weist, wie oben festgestellt, einen typischen hyperbelförmigen Verlauf auf. Punkt M stellt das Portfolio mit dem geringsten Risiko dar. Es existieren jedoch weitere effiziente Portfolios. Diese liegen auf dem oberen Ast der hyperbelförmigen Kurve und somit oberhalb von Punkt M. Bei diesen Portfolios spricht man von Minimum-Varianz-Portfolios. Der Teil der Kurve, auf dem diese Portfolios liegen, wird als Effizienzlinie bezeichnet.[7] Nur wenn sich ein Investor für ein Portfolio entscheidet, das auf dieser Effizienzlinie liegt, diversifiziert er richtig.[1]
Der untere Hyperbelast besteht ebensfalls aus Minimum-Varianz-Portfolios. Diese Portfolios sind jedoch im Vergleich zu den Portfolios auf dem oberen Hyperbelast ineffizient. Dies wird deutlich, wenn beispielhaft die Portfolios D und D´ in der Grafik " Wirkung des Korrelationskoeffizienten: Portfolio-Möglichkeitenkurven " miteinander verglichen werden: Zwar weisen beide Portfolios ein identisches Risiko auf, doch Portfolio D` ist durch einen höheren Ertragswert gekennzeichnet. Portfolio D`dominiert somit Portfolio D.
Effiziente Portfolios werden mit Hilfe von Lösungsalgorithmen und Computerprogrammen gefunden. Manuell ist dies durch einen bestimmten Optimierungsansatz möglich, jedoch bereits bei kleiner Wertpapieranzahl sehr aufwendig.[1]
Optimale Portfolios
Alle effizienten Portfolios liegen auf dem oberen Hyperbelast der Portfolio-Möglichkeitenkurve. Doch nicht alle effizienten Portfolios sind für einen Investor auch optimal. Die Auswahl des Portfolios hängt von der individuellen Risikoeinstellung des Investors ab. Die Risikoeinstellung wird mit Hilfe von Risikonutzenfunktionen dargestellt. Diese ordnen jeder Rendite-Risiko-Kombination einen bestimmten Nutzenwert zu. Unter Hinzunahme der Risikonutzenfunktion wird nur das Portfolio ausgewählt, welches dem Investor den maximalen individuellen Nutzen stiftet.
Jeder Investor hat eine eigene Einstellung zum Risiko, sodass jede Risikonutzenfunktion unterschiedlich aussieht. Alle Risikonutzenfunktionen haben jedoch den folgenden gemeinsamen Zusammenhang zwischen dem Nutzen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle U }
, der Rendite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mu}
und dem Risiko Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sigma}
: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle U= \operatorname {h} (\mu{,} \sigma)}
. An einem Beispiel soll die Auswahl eines optimalen Portfolios veranschaulicht werden.[7]
- Beispiel: [7] Es stehen zwei Portfolios mit den folgenden Rendite-Risiko-Kombinationen zur Auswahl:
| Rendite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mu\,} | Risiko Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sigma\,} | |
|---|---|---|
| Portfolio 1 | 6,0 % | 4,5 |
| Portfolio 2 | 7,5 % | 9 |
- Die Risikoeinstellung eines Investors wird mit dieser Risikonutzenfunktion dargestellt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle U= \mu - 0,02 (\sigma^2 + \mu^2 )\,}
. Welches Portfolio soll der Investor wählen?
- Zunächst müssen die Nutzenwerte berechnet und im Anschluss miteinander verglichen werden: Der Investor sollte Portfolio 1 wählen, da ihm dieses den größten Nutzen stiftet ( Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle U_1 > U_2\,}
).[7]
Die Risikonutzenfunktion lässt sich vereinfacht zweidimensional darstellen. Sie wird dann als Indifferenzlinie, Isonutzenkurve oder auch als Nutzenindifferenzkurve bezeichnet. Sämtliche Rendite-Risiko-Kombinationen, die auf einer Indifferenzkurve liegen, stiften den gleichen Nutzen, daher auch der Name.
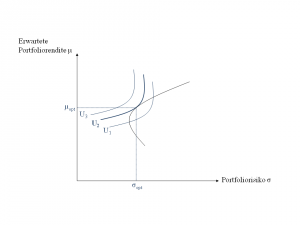
Die vollständige Präferenzstruktur eines Investors wird durch die Kurvenschar der Indifferenzkurven abgebildet. In der Grafik " Auffinden eines optimalen Portfolios " sind exemplarisch drei Indifferenzkurven dargestellt. Es gilt stets: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle U_3 > U_2 > U_1\,}
.[7] Das bedeutet, dass diejenige Indifferenzkurve, die vom Ursprung am weitesten entfernt ist, den höchsten Nutzen aufweist.[7]
Die Portfolio-Theorie geht von einem risikoscheuen Investor aus. Die Indifferenzkurven haben bei dieser Risikoeinstellung einen konvexen Verlauf. Für das Auffinden des optimalen Portfolios muss die Indifferenzkurve ermittelt werden, die vom Ursprung am weitesten entfernt ist und gleichzeitig die Effizienzlinie tangiert.[7]
In der Grafik " Auffinden eines optimalen Portfolios " ist diese Vorgehensweise dargestellt. Der Punkt mit den Koordinaten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (\sigma_{opt}|\mu_{opt} )\,}
stellt das Portfolio dar, das der Investor aufgrund seiner Risikonutzenfunktion wählen sollte, da ihm dieses Portfolio den größten Nutzen verspricht. [7]
Die Risikoeinstellungen der Anleger werden in der Praxis mit Hilfe von Fragebögen ermittelt. In diesen müssen Fragen bezüglich bestimmter hypothetischer Entscheidungssituationen beantwortet werden, deren Auswertung die individuelle Risikobereitschaft widerspiegelt.[7]
Branchendiversifikation und internationale Diversifikation
Das Aussehen und die Lage der Portfolio-Möglichkeitenkurve und somit auch der Effizienzlinie sind von der Anzahl der risikobehafteten Anlagen im Portfolio abhängig. Je größer die Anzahl der Anlagen im Portfolio ist, desto weiter links oben liegt die Portfolio-Möglichkeitenkurve im Ertrags-Risiko-Diagramm, desto günstiger ist somit das Portfolio hinsichtlich Renditeerwartung und Risiko. Um das Risikosenkungspotential zu realisieren, lässt sich das Portfolio vergrößern, indem der Investor nicht nur Anlagen aus seinem Land, sondern zusätzlich ausländische Assets in sein Portfolio aufnimmt. [2] Besteht das Portfolio des Investors nur aus inländischen Anlagen, verringert er den Umfang des Diversifikationseffektes. Das bedeutet, dass er durch die Hinzunahme ausländischer Assets eine günstigere Risiko-Ertrags-Relation erreicht hätte. [10] Solnik befasste sich als Erster mit dieser sogenannten internationalen Diversifikation, die in der Literatur auch als Länderdiversifikation bezeichnet wird. [2]
Assets eines Landes entwickeln sich homogen, da das politische Rahmengefüge auf diese in ähnlichem Maße einwirkt. Dabei handelt es sich beispielsweise um Geld-, Steuer- und Fiskalpolitik. Zwischen den Ländern existieren in dieser Hinsicht jedoch Unterschiede, sodass Assets verschiedener Länder einen niedrigen Korrelationskoeffizienten aufweisen. Somit wird bei einer internationalen Diversifikation in der Regel ein stärker ausgeprägter Diversifikationseffekt erreicht. [10]
Bei einer internationalen Diversifikation bestehen neben den spezifischen Risiken aus den jeweiligen Anlagen außerdem sogenannte Währungsrisiken. Diese Risiken lassen sich durch das Hedging mit Hilfe von Währungsfutures (engl. Currency Futures) ausschalten. Das Portfolio kann um diese Hedginginstrumente erweitert werden, sodass in der Konsequenz die Relation zwischen Risiko und Ertrag eines Portfolios zusätzlich verbessert wird.[2]
Aktiendiversifikation bedeutet jedoch nicht zwangsläufig, dass in ausländische Aktien investiert werden muss. Solange die Kursentwicklung heterogen verläuft, ist ein Deversifikationseffekt möglich. Dies kann bereits bei Investition in inländische Aktien unterschiedlicher Branchen der Fall sein.
- Beispiel: Wenn ein Investor in die Chemie-, Biotechnologie- und Pharmabranche investieren möchte und dabei Aktien der Pfizer Inc., Hoechst AG und der Novartis AG kauft, dann wird der Diversifikationseffekt wahrscheinlich schwach ausgeprägt sein, obwohl er Assets verschiedener Staaten gewählt hat. Dies liegt daran, dass es sich um nur eine Branche handelt und die Aktien einer Branche ähnlichen Risiken ausgesetzt sind. Der Investor hätte vermutlich einen besseren Diversifikationseffekt erzielt, wenn er sich für Aktien aus seinem Land, jedoch für Aktien aus verschiedenen Branchen entschieden hätte, beispielsweise für die BASF-, Volkswagen- und Siemens-Aktien.[2]
Viele empirische Studien sind der Frage nachgegangen, ob eine internationale Diversifikation oder eine Branchendiversifikation günstiger sei. Dabei diente Rolls Aufsatz als Ausgangspunkt. Aus diesem Aufsatz geht hervor, dass eine Länderdiversifikation im Prinzip immer eine Branchendiversifikation ist, da jedes Land seinen Schwerpunkt auf eine bestimmte Industriestruktur setzt.[2] Die Korrelation der Assets einzelner Branchen ist gering, sodass ein gut ausgeprägter Diversifikationseffekt erreichbar ist. [10]
Im Ergebnis unterstützen die empirischen Studien den Investor bei seiner Anlageentscheidung.[2]
Literatur
- Peter Albrecht, Raimond Maurer: Investment- und Risikomanagement, Schäffer-Poeschel Verlag Stuttgart, Stuttgart 2008, ISBN=978-3-7910-2827-9.
- Martin Bösch: Finanzwirtschaft - Investition, Finanzierung, Finanzmärkte und Steuerung, Verlag Franz Vahlen München, München 2009, ISBN=978-3-8006-3634-1.
- Günter Franke, Herbert Hax: Finanzwirtschaft des Unternehmens und Kapitalmarkt, Springer-Verlag, Berlin 2004, ISBN=3-540-40644-1.
- John C. Hull: Risk Management and Financial Institutions, Pearson Education, Inc., publishing as Prentice Hall 2004, ISBN=3-540-40644-1.
- Neil Doherty: Integrated Risk Management: Techniques and Strategies for Managing Corporate Risk, Verlag=McGraw-Hill, Inc., New York 2010, ISBN=978-0-13-800617-4.
- Söhnke M. Bartram, Gunter Defey: International Portfolio Investment: Theory, Evidence, and Institutional Framework, FINANCIAL MARKETS, INSTITUTIONS & INSTRUMENTS, Volume 10, Issue 3, S.85-155, August 2001.
Weblinks
Einzelnachweise
- ↑ 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 Hendrik Garz, Stefan Günther, Cyrus Moriabadi: Portfolio-Management - Theorie und Anwendung. 2. Auflage. Bankakademie e.V., Frankfurt am Main 1998, S. 17 f., 34-41, 47 f., 58, 139-141, ISBN 3-933165-09-1.
- ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 2,10 2,11 2,12 Klaus Spremann: Portfoliomanagement. 2. Auflage. Oldenbourg Wissenschaftsverlag GmbH, München 2003,
S. 22-26, 184-186, 191-193, 201-204, 302 f., ISBN 3-486-27269-1. Referenzfehler: Ungültiges<ref>-Tag. Der Name „Spremann“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. - ↑ 3,0 3,1 3,2 Investment www.bankert-finanz.de, abgerufen am: 27. November 2010.
- ↑ Der babylonische Talmud. Nach der ersten zensurfreien Ausgabe unter Berücksichtigung der neueren Ausgaben und des handschriftlichen Materials, ins Deutsche übersetzt von Lazarus Goldschmidt, Berlin 1929-1936, Bd. VII, S. 575.
- ↑ Shlomo Benartzi and Richard H. Thaler: Naive Diversification Strategies in Defined Contribution Saving Plans. In: American Economic Review , Los Angeles, 2000.
- ↑ Martin Bösch: Finanzwirtschaft - Investition, Finanzierung, Finanzmärkte und Steuerung.Verlag Franz Vahlen München, München 2009,S. 59, ISBN 978-3-8006-3634-1.
- ↑ 7,00 7,01 7,02 7,03 7,04 7,05 7,06 7,07 7,08 7,09 7,10 7,11 7,12 7,13 7,14 7,15 7,16 Horst Gräfer, Bettina Schiller, Sabrina Rösner: Finanzierung - Grundlagen, Institutionen, Instrumente und Kapitalmarkttheorie. 6. Auflage. Erich Schmidt Verlag GmbH & Co., Berlin 2008, S. 249-260, ISBN 978-3-503-10686-8.
- ↑ Neil A. Doherty, Andreas Richter: Moral Hazard, Basis Risk, and Gap Insurance . Vol. 69, No.1. The Journal of Risk and Insurance, 2002, S. 10.
- ↑ Robert S. Pindyck, Daniel L. Rubinfeld: Mikroökonomie. 6. Auflage. Pearson Studium, 2005, S. 231, ISBN 978-3-8273-7164-5.
- ↑ 10,0 10,1 10,2 Söhnke M. Bartram, Gunter Defey: International Portfolio Investment: Theory, Evidence, and Institutional Framework. Volume 10, Issue 3. FINANCIAL MARKETS, INSTITUTIONS & INSTRUMENTS, August 2001, S. 101 f.